01排序问题

特征：要钦定某个数判断是否符合什么条件；只跟相对大小有关。尤其是中位数、第几位上的数是谁。

[CQOI2009] 中位数

给出 \(1,2,...,n\) 的一个排列，统计该排列有多少个长度为奇数的连续子序列的中位数是 \(b\)。

Solution:¶

中位数，只跟相对大小有关，改变原序列：把大于 \(b\) 的数全部变为 \(1\)，小于 \(b\) 的数变为 \(-1\)，等于 \(b\) 则为 \(0\) 。
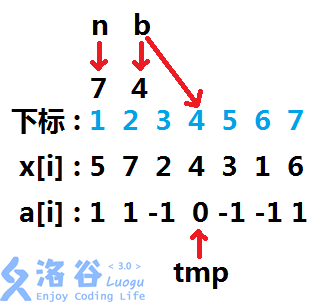
问题就变为求存在几个包含 \(b\) 的区间和为 \(0\) 。我们假设 \(tmp\) 为 \(b\) 的下标，原数组为 \(x\)，新数组为 \(a\) 。

Example:¶

7 4
5 7 2 4 3 1 6

能使结果成立的区间分别为 \([1,5]\) , \([1,7]\) , \([2,4]\) , \([4,4]\)。

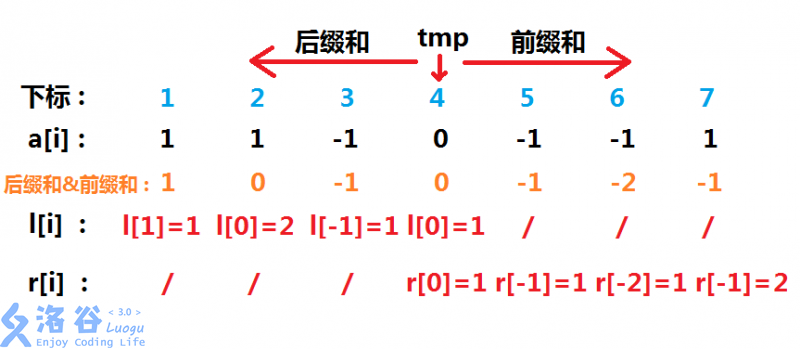
预处理出 \(tmp\) 左边的后缀和与右边的前缀和，开两个桶 \(l,r\) ，分别计数 \(tmp\) 左右两边前缀和的值的出现次数。于是左边的 \(l[x]\) 可以与右边的每一个 \(r[-x]\) 进行匹配。通过乘法原理，该值即为 \(l[x] \times r[-x]\)，由题意可知 \(-10^5 \le x \le 10^5\)，遍历所有的 \(x\) 即可，最终答案为 \(\sum_{i=min}^{max}l[i] \times r[-i]\) 。

值得注意的是，\(l[0]\) 和 \(r[0]\) 的初始值为 \(1\)，因为 \(b\) 是需要被算入的。当然，桶的下标不能是负数，所以我在每次操作时都加上了一个很大的数，即数据最大值 —— \(10^5\)，也可以用 \(STL\) 中的 \(map\) 解决问题，时间复杂度为 \(O(n)\) 。

std::map<int,int> l,r;
int main(){
    int n,b,pos;
    cin >> n >> b;
    for(int i=1;i<=n;i++){
        cin >> a[i];
        if(a[i]>b) a[i]=1;
        else if(a[i]==b) a[i]=0,pos=i;
        else a[i]=-1;
    }
    // 左右侧前缀和
    sum[pos]=0,l[0]=r[0]=1;
    for(int i=pos+1;i<=n;i++){
        sum[i]=sum[i-1]+a[i];
        r[sum[i]]++;
    }
    for(int i=pos-1;i>=1;i--){
        sum[i]=sum[i+1]+a[i];
        l[sum[i]]++;
    }
    long long ans=0;
    for(int i=-maxn;i<=maxn;i++){
        ans+=l[i]*r[-i];
    }
    cout << ans;
    return 0;
}

P2824 [HEOI2016/TJOI2016] 排序

给出一个 1 到 n 的排列，现在对这个排列序列进行 m 次局部排序，排序分为两种：

0 l r 表示将区间 \([l,r]\) 的数字升序排序
1 l r 表示将区间 \([l,r]\) 的数字降序排序

最后询问第 \(q\) 位置上的数字。

Solution:¶

线段树01排序 \(O(\log n)\) +二分答案

二分一个数 \(x\)，将大于等于 \(x\) 的数设为1，小于 \(x\) 的数设为0，用线段树跑出所有的操作，共 \(O(m\log n)\)。若此时最后第 \(q\) 位是1，说明答案一定大于等于这个数，否则则一定比这个数小。故二分边界 \(l=1,r=n+1\)。

bool check(int x){
    for(int i=1;i<=n;i++){
        if(a[i]<x) b[i]=0;
        else b[i]=1;
    }
    build(1,1,n);
    for(int i=1;i<=m;i++){
        int cnt = qry1(1,1,n,l[i],r[i]);
        if(cnt==0) continue;
        fill(1,1,n,l[i],r[i],0);
        if(op[i]==0){ // 升序
            fill(1,1,n,r[i]-cnt+1,r[i],1);
        }
        else {
            fill(1,1,n,l[i],l[i]+cnt-1,1);
        }
    }
    return qry1(1,1,n,q,q) == 1;
}

https://www.luogu.com.cn/problem/AT_agc006_d