差分约束¶
简介¶
差分约束系统,有 \(m\) 条约束条件,每条都为形如 \(x_a-x_b\geq c_k,x_a-x_b\leq c_k\) 或 \(x_a=x_b\) 的形式,判断该差分约束系统有没有解,求出其解。
题意转化:考虑建立最短路模型,差分约束系统中的每个约束条件 \(x_i-x_j\leq c_k\) 都可以变形成 \(x_i\leq x_j+c_k\),这与单源最短路中的三角形不等式 \(dist[y]\leq dist[x]+z\) 非常相似(x->y)
例题 luogu P1993 小 K 的农场¶
| 式子 | \(\leq\) | 连边 |
|---|---|---|
| \(x_a - x_b \geq c\) | \(x_b - x_a \leq -c\) | add(a, b, -c); |
| \(x_a - x_b \leq c\) | \(x_a - x_b \leq c\) | add(b, a, c); |
| \(x_a = x_b\) | \(x_a - x_b \leq 0, \space x_b - x_a \leq 0\) | add(b, a, 0), add(a, b, 0); |
例题 P4926[1007] 倍杀测量者¶
不考虑二分等其他的东西,差分系统 \(\frac{x_i}{x_j}\leq c_k\) 的求解方法:
对每个 \(x_i,x_j\) 和 \(c_k\) 取一个 \(\log\) 就可以把乘法变成加法运算,即 \(\log x_i-\log x_j \leq \log c_k\),这样就可以用差分约束解决了。
判定无解¶
由于 \(a_i\) 是一组最短路的解,那么只需判定最短路是否无解——判负环
SPFA 判负环:每次将一个点丢进队列里,相当于是对这一个点的所有出边进行松弛,那么只需要记录每个点的进队次数,若超过总节点数-1,说明松弛次数太多,有负环,无解;否则有解。
有超级源点——incnt[to]>=n+1时break;
无超级源点——incnt[to]>=n时break。
求解¶
如果跑完了spfa,则最终dis[1~n]的数即为一组解。
有推论:设向量 \(x=(x1,x2,\cdots,x_n)\)为差分约束系统 \(A_x\leq b\) 的一个解,设 \(d\) 为任意常数,则 \(x+d=(x_1+d,x_2+d,\cdots,x_n+d)\) 也是该差分约束系统的一个解。
由该推论,我们可以把或许求出的很怪异的不等式解变成正整数解,看起来更自然。
易错点¶
1.用错算法¶
由于 \(k\) 符号不确定,所以可能有负(正)权边,这也是为什么我们不能使用 dijkstra 算法,而只能使用 Bellman-Ford 或 SPFA 求最短(长)路的原因。
dijkstra 算法求最短(长)路为何不能用于负(正)权边
(如果您早就明白这是为什么,请自行跳过)
以求最短路为例,dijkstra 算法是利用贪心思想,每次用距离源点最近的、未讨论过的点去更新其他点的最短距离,有点类似于 bfs (宽度优先搜索)。
但当出现负权边时,后面讨论的点相较于已讨论的点,可能会距离源点更近,导致已讨论的点会被更新,却不会再次拿来讨论,此时 \(O(n^2)\) 的 dijkstra 算法就失效了。
不过,如果使用带有堆优化的时间复杂度为 \(O(nlog_{_2}m)\) 的 dijkstra 算法,它会退化成 SPFA 算法,相当于将 SPFA 算法中的队列换成堆,时间复杂度为 \(O(nmlog_{_2}m)\),显然超时。
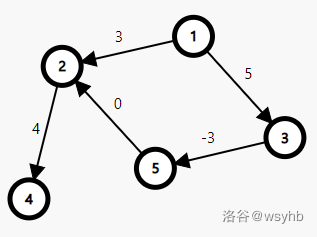
最后放一个例子,以便读者理解:
以 \(1\) 为源点,用 \(O(n^2)\) 的 dijkstra 算法求解单源最短路,所求得的 \(dis_{_4}\) 为 \(7\),即路径 \(1\) -> \(2\) -> \(4\)。而实际上 \(dis_{_4}\) 应该为 \(6\),即路径 \(1\) -> \(3\) -> \(5\) -> \(2\) -> \(4\)。
错误原因是 \(dis_{_2}=3<dis_{_3}=5\),所以先讨论了点 \(2\) ,将点 \(4\) 更新,而之后点 \(5\) 去更新点 \(2\),点 \(2\) 却不会再用新的 \(dis_{_2}=2\) 去更新点 \(4\) 了。
2.图不连通¶
这里可能会存在点之间既不直接约束也不间接约束的情况,在建图上的体现就是图不连通。
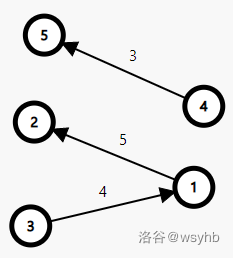
举个简单的例子:(\(n=5\),\(m=3\))
依据第一种思路建图如下:
此时无论以 \(1\) , \(2\) , \(3\) , \(4\) , \(5\) 哪个点作为源点,都无法计算出正确答案。(对于 SPFA)
理由是以其中一个点作为源点,只能计算出这个点所在连通块的答案,并没有计算其他连通块的答案。
SPFA解决方案
-
一开始将所有点放入队列中而不是只放一个起点,这样每个点都被作为起点讨论过。
-
建一个虚拟源点 \(0\),从这个虚拟源点向其他所有点都连一条长度为 \(0\) 的边,以虚拟源点为起点放入队列,这样的效果与前一种完全相同。但是不要忘了把边开大!!!!!!